Suppose a Random Walk Start at the Origin Probability That It Will Ever Touch the Xaxis Again
Random Walks
A walk?" said Catharine. "I human foot in front end of the other," said Newt, "through leaves, over bridges—"
Kurt Vonnegut (Long Walk to Forever)

Motivation
Now that nosotros have a handle on what a stochastic process actually is, permit's explore this crucial class of processes, both analytically and via simulation in R. Nosotros can use the fundamental attributes and topics that we learned in the final affiliate to solidify our frame of reference.
Gaussian Random Walk
Let'south first with a elementary stochastic process that we've already met: a Gaussian Random Walk, which is substantially a series of i.i.d. \(Due north(0, 1)\) random variables through time:
\[X_0 = 0\] \[X_t = X_{t - 1} + \epsilon_t\]
Where \(t = 1, 2, ...\) and \(\epsilon_t\) is a series of i.i.d. \(Due north(0, i)\) random variables.
Let'south investigate the Gaussian Random Walk farther with some of the properties we've learned well-nigh.
# replicate fix.seed(0) # generate a Gaussian Random Walk information <- data.table(t = c(0, seq(from = 1, to = 100, by = 1)), replicate(c(0, cumsum(rnorm(100))), n = 100)) data <- melt(data, id.vars = "t") ggplot(data, aes(x = t, y = value, col = variable)) + geom_line() + ggtitle("100 Simulations of a Gaussian Random Walk") + theme_bw() + theme(legend.position = "none") + xlab("t") + ylab("X_t") + geom_hline(yintercept = 0) 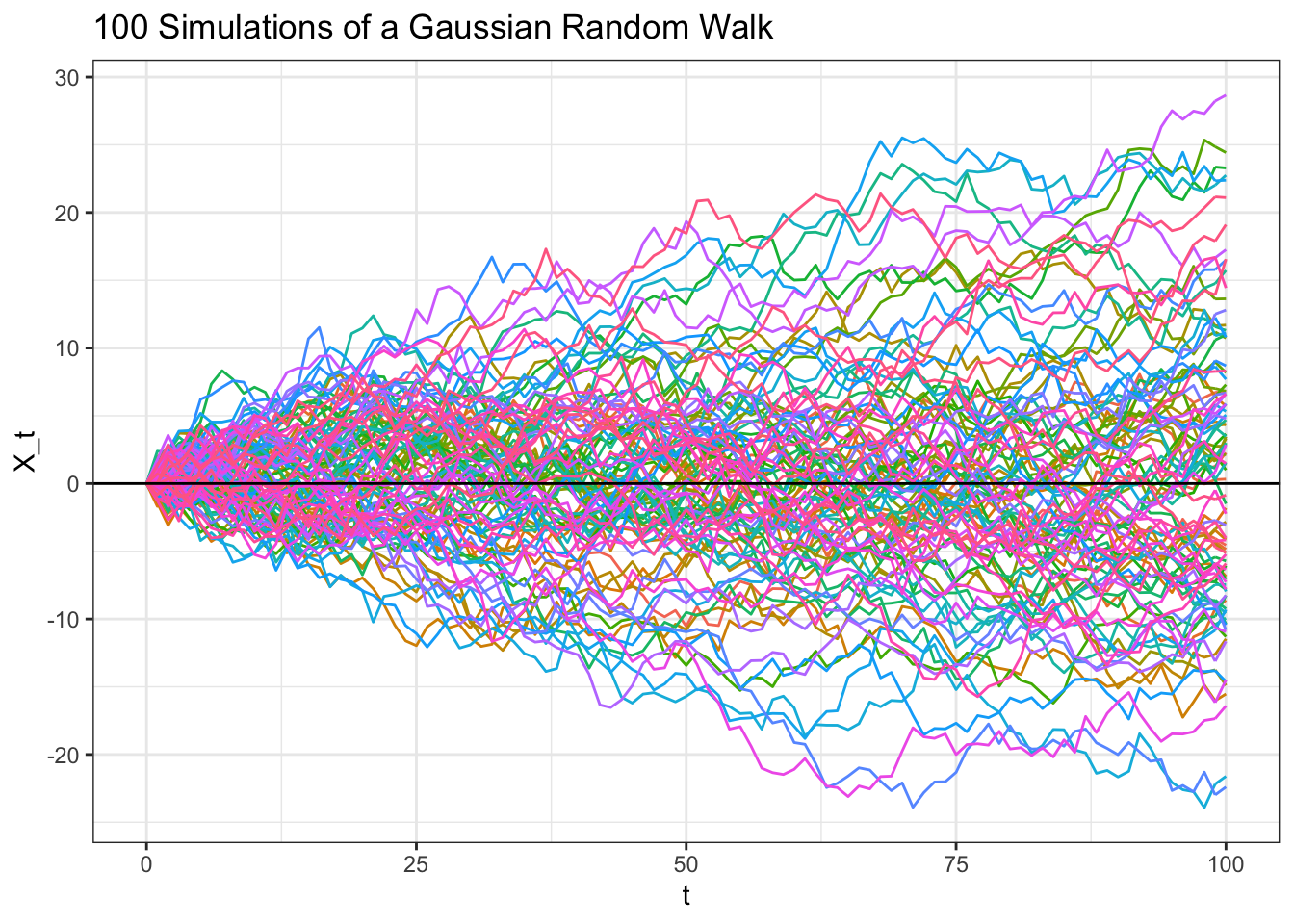
Strong Stationarity
Retrieve, a stochastic process is strongly stationary if:
\[F_{t_1, t_2, ..., t_n} = F_{t_1 + k, t_2 + one thousand, ..., t_n + k}\]
For all \(k\), \(n\) and sets of time intervals \(t_1, t_2, ...\) in the stochastic procedure. Colloquially, the distributional properties of the process don't change over fourth dimension.
Permit's start with a simple case. Is \(F_{t_{ane}}\) equal to \(F_{t_{5}}\), for instance?
We can first by expanding \(X_t\). We have that, past definition:
\[X_t = X_{t - 1} + \epsilon_t\]
Plugging in for \(X_{t-1}\), nosotros have:
\[X_{t - 2} + \epsilon_{t - 1} + \epsilon_t\]
Continuing in this way until nosotros get to \(X_0 = 0\), nosotros take:
\[X_0 + \epsilon_1 + ... + \epsilon_{t - i} + \epsilon_t\]
Or simply:
\[\epsilon_1 + ... + \epsilon_{t - ane} + \epsilon_t\]
Since each \(\epsilon\) is a Normal random variable (each i.i.d. with expectation \(0\) and variance \(i\)), and the sum of Normals is Normal, nosotros take:
\[X_t \sim N(0, t)\]
Notation that this is a similar construct to our Brownian motion; the difference is that the Gaussian Random Walk is only defined on detached points (specifically, \(0, i, 2...\)) where the Brownian Motility is continuous (defined for \(t \geq 0\)). This result is besides intuitive given the shape of the many paths for the Gaussian Random Walk that we sampled. Curl up to the graph above and imagine taking vertical cross sections (depict a vertical line and look at the distribution of the path intersections). The variance of these intersections grows with time (this is the variance \(t\) at play) while the hateful stays at nada (as above, \(X_t\) has a mean of \(0\)).
Anyways, that means that \(F_{t_{1}}\) is the CDF of a \(N(0, 1)\) random variable, while \(F_{t_{5}}\) is the CDF of a \(Northward(0, v)\) random variable. These are dissimilar CDFs (even though the structure is the same, the variance term is different) and thus the Gaussian Random Walk is not strictly stationary (intuitively, the distribution changes over fourth dimension because the variance increases).
Weak Stationarity
Recall that a procedure is weakly stationary if these three weather are satisfied:
- The mean of the process is constant. That is, \(E(X_t) = \mu\) (where \(\mu\) is some constant) for all values of \(t\).
- The second moment of \(X_t\), or \(E(X_t ^ two)\), is finite.
- We have:
\[Cov(X_{t_1}, X_{t_2}) = Cov(X_{t_1 - k}, X_{t_2 - g})\]
For all sets of \(t_1, t_2\) and all values of \(k\).
Let's investigate these conditions for the Gaussian Random Walk.
- Beginning, nosotros can calculate the expectation using a similar expansion to our exercise above. Plugging in for \(X_t\), we have:
\[Eastward(X_t) = E(X_{t - ane} + \epsilon_t)\]
Plugging in over again for \(X_{t - ane}\), we have:
\[Due east(X_t) = E(X_{t - 2} + \epsilon_{t - i} + \epsilon_t)\]
This continues until we finally hitting \(X_0\), which is simply \(0\). Nosotros take:
\[E(X_t) = Eastward(X_0 + \epsilon_1 + ... + \epsilon_{t - 1} + \epsilon_t)\]
And since each \(\epsilon_t\) is i.i.d. \(North(0, i)\), this all simply reduces to \(0\). Therefore, the expectation is indeed abiding at zero (yep, information technology's truthful that nosotros already showed this, but it can't injure to explore the derivation again!).
- We have already shown that \(E(X_t) = 0\), so nosotros accept:
\[Var(X_t) = E(X^2)\]
Since \(East(X_t) ^ 2 = 0\). Since each pace in the process is i.i.d., we tin can easily calculate the variance with a similar approach to the expectation. Plugging in our full expansion of \(X_t\), nosotros have:
\[Var(X_t) = Var(X_0 + \epsilon_1 + ... + \epsilon_{t - i} + \epsilon_t)\]
\(X_0\) is a abiding and each \(\epsilon\) term has a variance of 1, and then this reduces to:
\[Var(X_t) = Eastward(Ten^2) = t\]
Of course, we could have just used the fact that \(X_t \sim N(0, t)\), as shown higher up, instead of solving the variance in expectation in these first ii parts; yet, the practice is good!
Anyways, nosotros accept shown the second moment to be finite!
- Nosotros already saw that the variance of this procedure is not constant. Allow'southward consider the covariance:
\[Cov(X_{t - k}, X_t)\]
We can use this key property of covariance…
\[Cov(X + Y, Z) = Cov(X, Z) + Cov(Y, Z)\]
…to solve this problem. Let'southward utilize the expansion for \(X_t\) that we accept employed to slap-up success thus far:
\[Cov(X_{t - k}, X_t) =\] \[Cov(X_0 + \epsilon_1 + ... + \epsilon_{t - grand}, X_0 + \epsilon_1 + ... + \epsilon_t)\]
Recall that \(X_0 = 0\) and that a constant has no covariance, so these terms drop out. Further, since each \(\epsilon\) term is i.i.d., \(Cov(\epsilon_i, \epsilon_j) = 0\) for \(i \neq j\). We are simply left, then, with:
\[Cov(\epsilon_1, \epsilon_1) + Cov(\epsilon_2, \epsilon_2) + ... + Cov(\epsilon_{t - yard}, \epsilon_{t - k})\] \[= Var(\epsilon_1) + Var(\epsilon_2) + ... + Var(\epsilon_{t - 1000})\]
And, since each variance is i, we are simply left with:
\[Cov(X_{t - k}, X_t) = t - k\]
Since our Covariance clearly depends on \(t\) and \(thousand\) (the larger \(yard\) is, the lower the covariance; this is intuitive because \(X_{t - k}\) is farther from \(X_t\) when \(k\) is large), we exercise not satisfy the tertiary condition of weak stationary. Therefore, this Gaussian Random Walk is not weakly stationary.
Martingale
Recall that a stochastic process is a martingale if:
\[Eastward(X_{due north + 1} | X_1, ..., X_n) = X_n\]
For a Gaussian Random Walk, at every increment we are calculation a random variable (an \(\epsilon\) term) with an expectation of \(0\). Therefore, the expectation of \(X_{north + 1}\) is merely \(X_n\) (since we are adding something that we look to be nil!).
Therefore, the Gaussian Random Walk is a martingale.
Markov
Call up that a stochastic process \(X_t\) is Markov if:
\[P(X_t|X_1, X_2, ..., X_{t - 1}) = P(X_t | X_{t - })\]
That is, the probability distribution of \(X_t\), given the unabridged history of the procedure up to fourth dimension \(t\), only depends on \(X_{t - 1}\). As we discussed in the final chapter, a Gaussian Random Walk is Markov!
Unproblematic Random Walk
We can continue our written report of random walks with a more fundamental structure; a uncomplicated random walk \(X_t\) is a stochastic procedure where:
\[X_t = \sum_{i = 1}^t Y_i\]
Where \(X_0 = 0\). We permit the \(Y\) random variables be i.i.d. such that \(P(Y_i = 1) = p\) and \(P(Y_i = -1) = 1 - p = q\) (that is, \(Y\) tin can just equal \(ane\) with probability \(p\) or \(-1\) with probability \(q = 1 - p\)). We tin can envision, then, \(X_t\) but moving upward or down \(ane\) at each time bespeak, governed past the probability \(p\) (of moving up \(ane\); remember that \(q\), or \(one - p\), is the probability of moving downwards \(i\)). Let's simulate a simple random walk to visualize its action:
# replicate set.seed(0) # function to generate random walks FUN_simplewalk <- function(t, p) { x <- 0 for (i in one :t) { ten <- c(10, x[length(x)] + sample(c(- 1, 1), 1, prob = c(i - p, p))) } return(ten) } # generate and visualize data <- data.tabular array(t = 0 : 100, 10 = FUN_simplewalk(100, .6)) ggplot(data, aes(x = t, y = ten)) + geom_line() + theme_bw() + ylab("X_t") + ggtitle("Uncomplicated Random Walk for 100 steps (p = .6)") 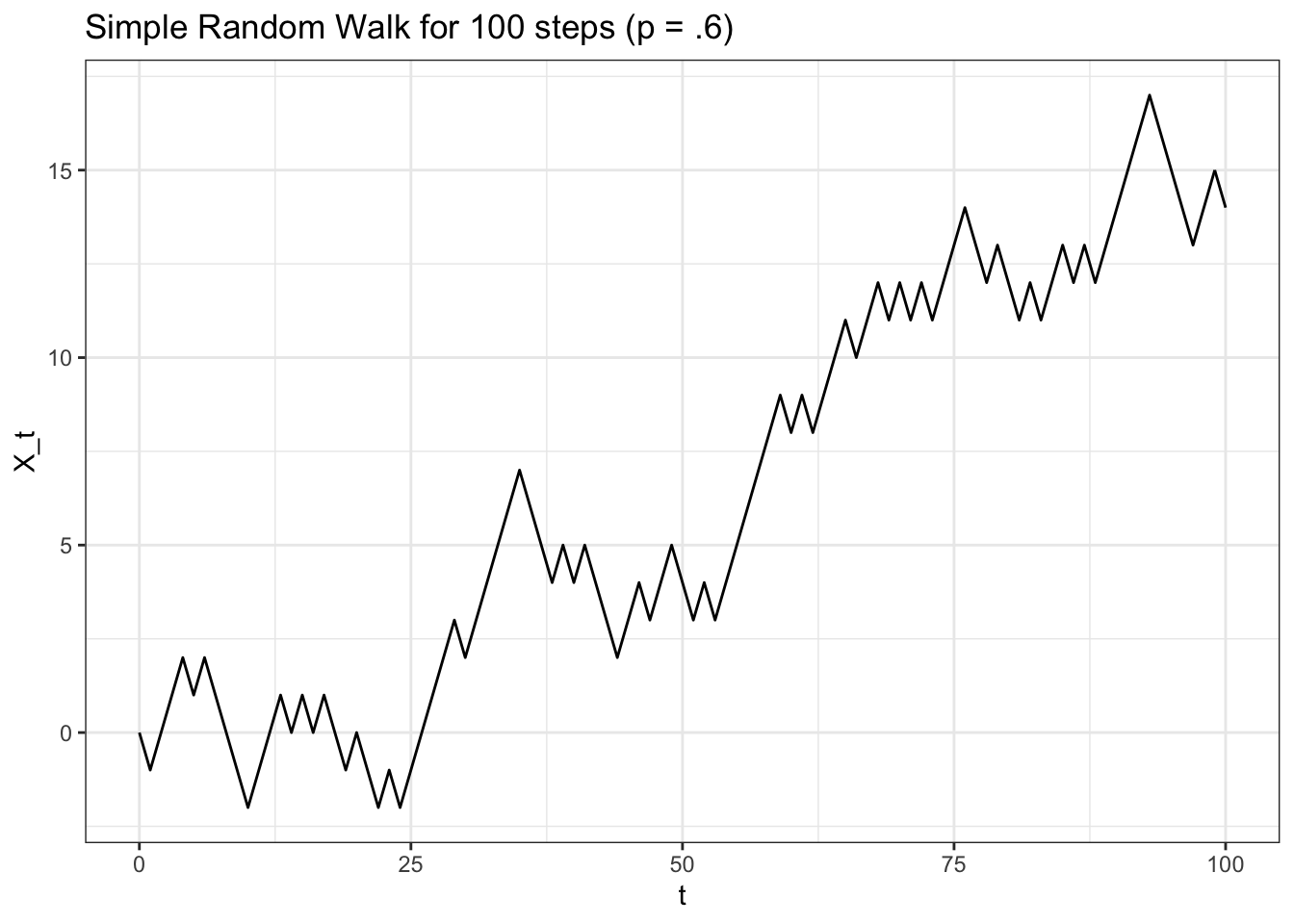
In this case, \(p = .vi\), and so there is no surprise that the random walk drifts up (most of the moves will be 'upwards moves!'). A symmetric unproblematic random walk is one where, well, \(p = .v\), then that we have symmetric probabilities of moving up or down.
We can hands summate some of the key metrics of \(X_t\). Let's commencement with the expectation (think that \(X_0 = 0\)):
\[East(X_t) = Eastward(X_0 + Y_1 + Y_2 + ... + Y_n)\] \[ = E(Y_1) + E(Y_2) + ... + E(Y_n)\]
Think that each \(Y_i\) term is i.i.d. with probability \(p\) of taking on the value of \(one\) and probability \(1 - p\) of taking on the value \(-1\), then the expectation of each \(Y_i\) term is:
\[E(Y_i) = p \cdot ane + (1 - p) \cdot (-1)\]
\[= p + p - 1 = 2p - one\]
Plugging in to \(Due east(X_t)\) above:
\[Eastward(X_t) = t(2p - 1)\]
This expectation is intuitive: if \(p = 1/2\), and so \(E(X_t) = 0\), which makes sense past symmetry (if the random walk is as likely to go up or downwardly, then we expect it to not motion in the long run!). If we accept \(p > 1/2\), and then \(E(X_t) > 0\), which makes sense because the random walk 'drifts' upwards equally nosotros saw above (and, of course, for \(p < ane/2\), we have \(E(X_t) < 0\) for the aforementioned reason).
We tin as well summate the variance:
\[Var(X_t) = Var(Y_1 + Y_2 + ... + Y_n)\]
\[Var(X_t) = Var(Y_1) + Var(Y_2) + ... + Var(Y_n)\]
We tin can add the variances considering each \(Y_i\) term is i.i.d. We can discover the variance of \(Y_i\) by using the following relation:
\[Var(Y_i) = E(Y_i^2) - \big(Due east(Y_i)\large)^ii\]
We already have \(Due east(Y_i)\), and tin can calculate \(E(Y_i^2)\) by simply looking at the structure of \(Y_i^ii\). Since \(Y_i\) merely takes on values \(1\) and \(-1\), we have that \(Y_i^2\) will always take on the value one. Nosotros therefore have, plugging in \(E(Y_i) = 2p - 1\) from before:
\[Var(Y_i) = i - (2p - one)^two\]
\[= 1 - (4p^ii - 4p + 1)\] \[= i - 4p^two + 4p - 1\] \[=4p - 4p^ii\] \[=4p(1 - p)\]
Which means that the variance of \(X_t\) is merely \(t2p(ii - p)\).
Let'due south check our expectation and variance past simulating many paths of unproblematic random walks:
# replicate set up.seed(0) # define parameters and generate results p <- .55 t <- 100 results <- replicate(FUN_simplewalk(t = t, p = p), northward = 1000) results <- results[t + 1, ] # expectations should match t * (2 * p - one); hateful(results) ## [1] 10 ## [1] nine.826 # variances should friction match t * 4 * p * (1 - p); var(results) ## [1] 99 ## [1] 94.61234 Our analytically results expect shut to the simulated results!
Properties
We can almost immediately say that the elementary random walk is not strongly stationary considering of a similar argument to the Gaussian random walk higher up: the variance that we calculated higher up is a function of \(t\) and thus increases with fourth dimension, pregnant that the distribution of \(X_5\) will exist different, than, say, the distribution of \(X_{17}\) (we have that \(Var(X_{17}) > Var(X_5)\)).
Further, we can utilize a similar approach as before to evidence that the simple random walk is also not weakly stationary. Consider the covariance:
\[Cov(X_{t - k}, X_t)\]
Plugging in that each \(X_t\) is a sum of \(Y_i\) random variables:
\[=Cov(Y_1 + ... + Y_{t - k}, Y_1 + ... + Y_t)\]
Since the \(Y_i\) terms are all i.i.d., using the property from higher up (scroll to the Gaussian random walk weak stationarity exercise for more elaboration) we have:
\[= Var(Y_1) + Var(Y_2) + Var(Y_{t - k})\]
Again, each \(Y_i\) term has the aforementioned variance (the terms are i.i.d.), and so we have:
\[= (t - k) Var(Y_1)\]
Therefore, because the covariance clearly depends on \(t\) (we multiply by \(t - k\)), this process is not weakly stationary.
Let's perform the crucial adding to determine if \(X_t\) is a martingale; that is, if this condition holds:
\[E(X_{t + 1} | X_1, ..., X_t) = X_t\]
We can calculate the provisional expectation:
\[E(X_{t + 1} | X_t) = X_t + 1 \cdot p - 1 \cdot(1 - p)\]
Since, conditioned on \(X_t\), we either move up \(1\) with probability \(p\) or down \(1\) with probability \(1 - p\). This only equals \(X_t\) if \(p - (1 - p) = 2p - 1 = 0\), which is only the example if \(p = 1/2\). Therefore, \(X_t\) is a martingale only if we have \(p = 1/ii\). This makes sense; we but expect a move of zilch if nosotros take symmetric probabilities of moving up and down (otherwise nosotros accept drift up or down).
Finally, we can see that a elementary random walk is Markov; for the distribution of \(X_t\), we have that \(X_{t - one}\) provides all of the information from the history of \(X_t\) that we need. Like to the Gaussian random walk, as long as we know where we were on the previous step, information technology doesn't matter how we got there; our distribution for the next stride is still the aforementioned.
Barriers
We've been dealing with unrestricted uncomplicated random walks where, every bit the name implies, there are no limits to where the random walk goes! We tin can add bulwark that either 'absorb' or 'reflect' the random walk.
If a random walk hits an absorbing barrier it is, well, absorbed. The random walk finishes and the process sits at that absorbing barrier for the rest of time. Formally, if \(a\) is an absorbing barrier, and \(X_t\) hits \(a\) for the kickoff time at time \(k\), so \(X_t = a\) for \(t \geq thousand\) with probability \(1\).
Random walks with arresting barriers are withal not weakly stationary or strongly stationary (for essentially the same reasons that unrestricted random walks are not weakly stationary or strongly stationary). Random walks with absorbing barriers are still Markov and still Martingale: even if we are trapped in the absorbing state, the Markov belongings holds (we know where nosotros will be in the adjacent stride, then conditioning on the entire history of the process gives no more than information than conditioning on simply the previous pace), and the process is nonetheless a Martingale (the expected value of the next step is just the electric current footstep, because we know that the next footstep will be the current step; we are in the arresting state!).
If the random walk hits a reflecting bulwark it is, well, reflected. The random walk 'bounces' dorsum from the bulwark to the value below (or in a higher place) the barrier. For instance, if \(r_{up}\) is an upper reflecting barrier and \(r_{down}\) is a lower reflecting variable, then for any \(X_t = r_{upward}\) (whenever nosotros hit the upper reflecting bulwark) nosotros have \(X_{t + i} = r_{upward} - 1\) with probability \(i\), and similarly for any \(X_t = r_{down}\) we take \(X_{t + one} = r_{downward} + 1\) with probability \(1\).
Again, reflecting barriers are still not weakly stationary or strongly stationary (for, again, much the same reasons). They are still Markov, since, even if nosotros are at the reflecting barrier, the most recent value in the process gives us every bit much information equally the entire history of the process. These random walks are not Martingales, though, since if we are the reflecting barrier, we know that the next value will be unlike from the value that we are currently at.
Behavior
Some key questions arise naturally when we consider random walks (in this department, nosotros will be discussing unrestricted simple random walks unless otherwise specified). For example, ane might ask what the probability is of the random walk ever reaching a certain value. For example, if we take a simple random walk with \(p = .6\), what is the probability that the random walk ever hits \(-10\)? We know that the random walk with drift upwards as fourth dimension passes, just volition it hit \(-10\) first?
Let's define \(P_k\) as the probability that a random walk always reaches the value \(k\). We accept:
\[P_k = P_1^g\]
That is, the probability that the random walk ever reaches \(k\) is just the probability that the random walk ever reaches \(ane\), to the power of \(k\). This makes sense, because we tin can think of getting to \(yard\) as essentially getting to \(1\) (which has probability \(P_1\)), but \(g\) times. Since each stride in the random walk is independent, we can simply heighten the probability to the power of \(k\).
We can focus, so, on finding \(P_1\). In this case, information technology will exist useful to utilise first step analysis, or conditioning on the kickoff footstep in the random walk and working out our probability from at that place. More formally:
\[P_1 = p P_1|U + qP_1 | D\]
Where \(P_1|U\) is the probability of reaching \(1\) given that the first step in the random walk is an 'Upwardly' move and \(P_1|D\) is the probability of reaching \(i\) given that the first pace in the random walk is a 'Down' move. This becomes:
\[P_1 = p + qP_2\]
Since if we move up on the first move and then we are at \(i\), and thus the probability of hitting \(1\) is, well, \(1\). If we motility down on the offset move, then the probability of striking \(1\) is at present \(P_2\), because nosotros take to become up \(2\) (from \(-one\)) to hit \(1\) now! We can plug in \(P_1^two\) for \(P_2\) using our equation to a higher place, which gives:
\[P_1 = p + qP_1^2\]
\[qP_1 ^ 2 - P_1 + p = 0\]
We can discover roots with the quadratic equation:
\[\frac{1 \pm \sqrt{1 - 4qp}}{2q}\]
The \(\sqrt{1 - 4pq}\) term is a bit tough to piece of work with, so we volition use a little flim-flam. We know that \(one = p + q\), and thus \(1^2 = one = (p + q)^2 = p^2 + q^2 + 2pq\). If nosotros take:
\[1 = p^two + q^2 + 2pq\]
And decrease \(4pq\) from both sides, we get:
\[i - 4pq = p^2 + q^2 - 2pq\]
So, nosotros can just plug in \(p^2 + q^ii - 2pq\) for \(1 - 4pq\), and this nicely factors to \((p - q)^2\) (technically, the foursquare root of \((p - q)^2\) is \(|p - q|\), since just \(p - q\) tin can be negative and the square root of something tin can't be negative; we won't accept to worry virtually that in this case, though, as you will see). We are left with:
\[\frac{1 + \pm p - q}{2q}\]
In the \(+\) case, nosotros accept:
\[\frac{ane + p - 1 + p}{2q} = \frac{2p}{2q} = \frac{p}{q}\]
In the \(-\) case, we have:
\[\frac{ane - p + 1 - p}{2q} = \frac{2q}{2q} = 1\]
And so our two roots are \(\frac{p}{q}\) and \(1\). In our case, when we have \(p > q\), we will utilize \(1\) every bit our root (since \(\frac{p}{q} > 1\) in this instance; this is why we didn't have to worry virtually the absolute value earlier!). The \(\frac{p}{q}\) makes sense; the lower that \(p\) gets, the lower the probability of hitting \(1\) gets.
And so, we found that \(P_1 = \frac{p}{q}\) when \(p < q\) and \(P_1 = 1\) when \(p \leq 1/2\). Using \(P_k = P_1^1000\), we simply have \(P_k = (\frac{p}{q})^k\) when \(p < q\) and \(P_k = 1\) when \(p \leq 1/2\) for \(k > 0\). That is, we volition definitely hit \(thou\) if \(p\geq 1/2\), whereas we might striking \(k\) if \(p < 1/two\) (with probability \((\frac{p}{q})^k\), which is less than \(1\)).
Note that this effect is symmetric to the downside; that is, \(P_k\) for \(k < 0\) is \((\frac{q}{p})^k\) for \(p > ane/two\) and \(one\) for \(p \leq 1/two\). Also note that this gives an interesting result: if \(p = ane/2\), so the probability that the random walk hits whatever value is \(1\); that is, we are certain that the random walk will striking all values eventually!
Let'south test this probability with a simulation with \(p = .3\), where the probability of hitting, say, \(two\) is \((\frac{.3}{.7})^2 = .184\). Naturally, we can't permit our simulation run forever; we'll just permit the random walk run long plenty and so that, if information technology hasn't hit \(2\) by that bespeak, it probably never will (it probable will be far enough on the negative side of \(0\) that it volition never climb back upward to \(2\)).
# replicate set.seed(0) # ascertain parameters and generate results p <- .3 t <- 75 results <- replicate(FUN_simplewalk(t = t, p = p), northward = 100) # how many become above ii? mean(apply(results, 2, max) >= two) ## [1] 0.19 # visualize data <- data.tabular array(t = ane :(t + one), results) information <- cook(data, id.vars = "t") ggplot(data, aes(x = t, y = value, col = variable)) + geom_line(alpha = 1 / 4) + theme_bw() + theme(legend.position = "none") + geom_hline(yintercept = ii, linetype = "dashed") + geom_hline(yintercept = 0) + xlab("t") + ylab("X_t") + ggtitle("How many random walks hit ii for p = .half-dozen?") 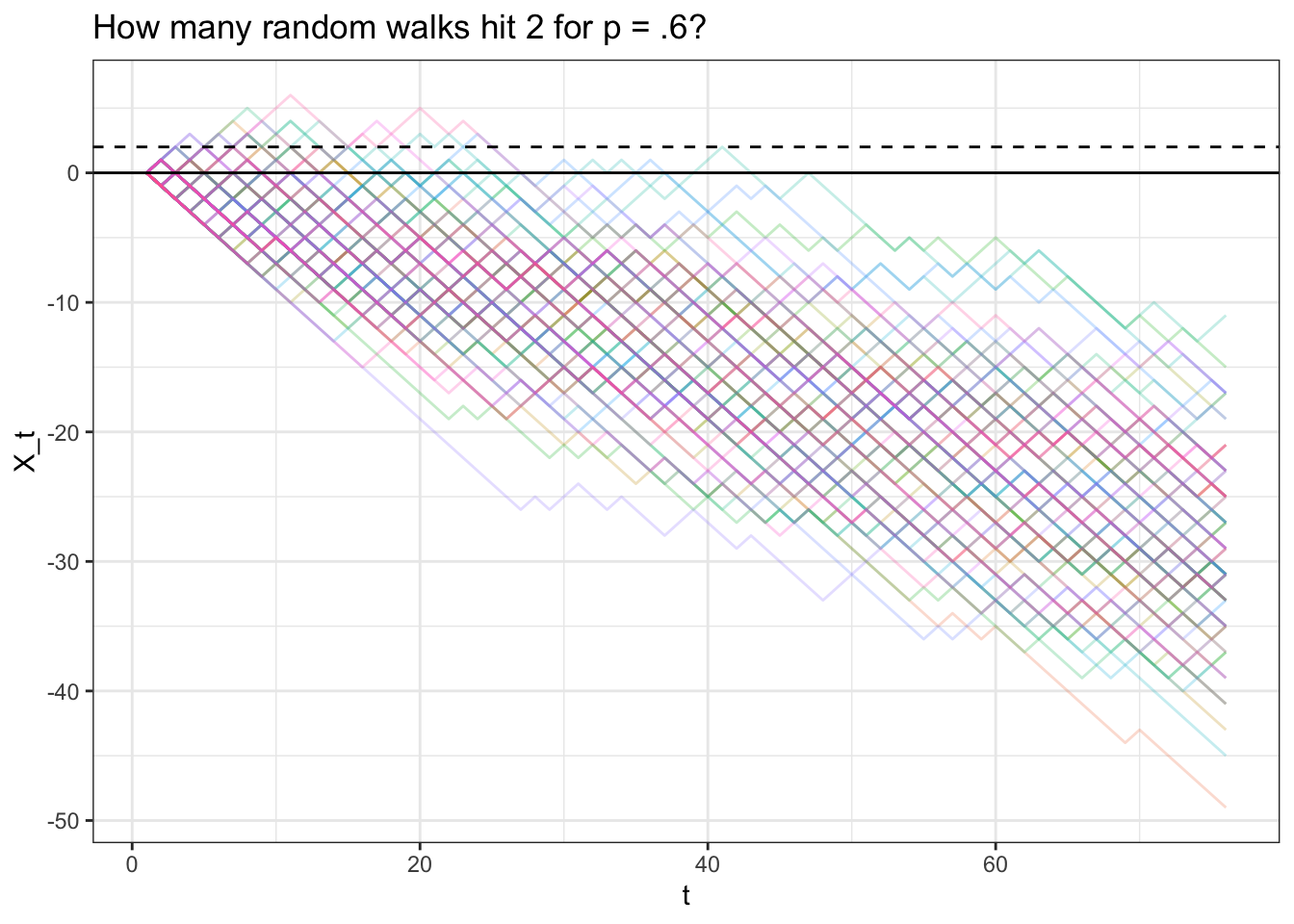
We run into that .xix of the simulations hit \(2\), which is close to our analytically event!
Here's a video walkthrough of this type of problem:
Click here to watch this video in your browser
Finally, now that nosotros accept a handle on the probability of hitting a certain value, allow'southward try to discover the expected time until nosotros hit a specific value. Permit's define \(T_k\) as the amount of fourth dimension it takes to go from \(0\) to \(thou\) (where \(k > 0\)) for a unproblematic, unrestricted random walk. We are interested in \(Eastward(T_k)\), which we tin luckily split into simpler terms:
\[E(T_k) = East(T_1) + E(T_1) + ... Due east(T_1) = kE(T_1)\]
This equation holds because we tin can retrieve of going up to the value \(g\) as simply going upwardly to the value \(ane\), but \(k\) times (to analyze, we don't mean hit \(1\) a total of \(g\) times, but hitting \(ane\), so \(two\), etc. until nosotros are up to \(grand\)).
Let's use showtime step analysis once again to attempt to detect \(E(T_1)\):
\[E(T_1) = 1 + p\cdot 0 + qE(T_2) = 1 + 2q Eastward(T_1)\]
The \(1\) comes from, well, taking the first stride. The \(p \cdot 0\) term is when the random walk goes upward one step with probability \(p\), hits \(1\) and thus has \(0\) more time expected until information technology hits \(1\). Finally, we accept \(East(T_2) = 2E(T_1)\) from our previous equation.
We're thus left to solve the equation:
\[East(T_1) = 1 + 2q E(T_1)\]
Let's commencement with the case where \(p < q\). We know from the previous section that, if \(p < q\), the probability of ever hit \(1\) is \(\frac{p}{q} < 1\). That ways that, with some not-zero probability (specifically, \(ane - \frac{p}{q}\)), the process volition never hit \(ane\), and thus take an infinite amount of time (considering it will never hit \(1\)). Therefore, since there is a nonzero probability of an infinite waiting time, the expectation of the waiting time is simply \(\infty\) (think about it: when we perform the calculation for expectation, nosotros will have some non-null probability times \(\infty\), which is just \(\infty\)).
When \(p = 1/2\), we merely accept:
\[Eastward(T_1) = 1 + E(T_1)\]
Which, of class, ways that \(Due east(T_1)\) is once more \(\infty\), since if you add \(ane\) to \(\infty\) you go \(\infty\).
Finally, if \(p > q\), we become:
\[E(T_1) = one + 2q Eastward(T_1)\]
\[E(T_1) - 2qE(T_1) = 1\]
\[East(T_1)(1 - 2q) = 1\] \[Due east(T_1) = \frac{one}{1 - 2q}\]
We take: \[1 - 2q = 1 - 2(ane - p) = 1 - 2 + 2p = p + p - one = p - q\]
Plugging this in, we go:
\[E(T_1) = \frac{one}{p - q}\]
So, therefore, if we recollect that \(Eastward(T_k) = kE(T_1)\), we have that when \(p \leq i/2\), \(E(T_k) = \infty\) for \(k > 0\) and when \(p > q\) we take \(East(T_k) = \frac{k}{p - q}\).
Let's simulate a bunch of paths and see if this expectation makes sense. Nosotros will try \(k = 5\) and \(p = .55\) which, co-ordinate to \(E(T_k) = \frac{k}{p - q}\), should have an expected 'hitting time' of \(\frac{5}{.55 - .45} = fifty\).
# replicate set.seed(0) # define parameters and generate results p <- .55 t <- 500 results <- replicate(FUN_simplewalk(t = t, p = p), n = 100) # see how long it took to go to 5 results_exp <- apply(results, 2, function(x) { # hit 5 if (max(ten) >= v) { return(min(which(10 == five)) - one) } render(502) }) # should match v / (p - (1 - p)); hateful(results_exp) ## [i] 50 ## [one] 49.48 # end all the results afterwards it hits v for (i in 1 : ncol(results)) { results[(results_exp[i] + 2): nrow(results), i] <- - 10000 } # visualize data <- data.table(t = ane :(t + 1), results) information <- cook(information, id.vars = "t") information <- data[value > - 10000] ggplot(information, aes(x = t, y = value, col = variable)) + geom_line(alpha = 1 / four) + theme_bw() + theme(legend.position = "none") + geom_hline(yintercept = v, linetype = "dashed") + geom_hline(yintercept = 0) + geom_vline(xintercept = 50) + xlab("t") + ylab("X_t") + ggtitle("How long until we striking five for p = .55?") 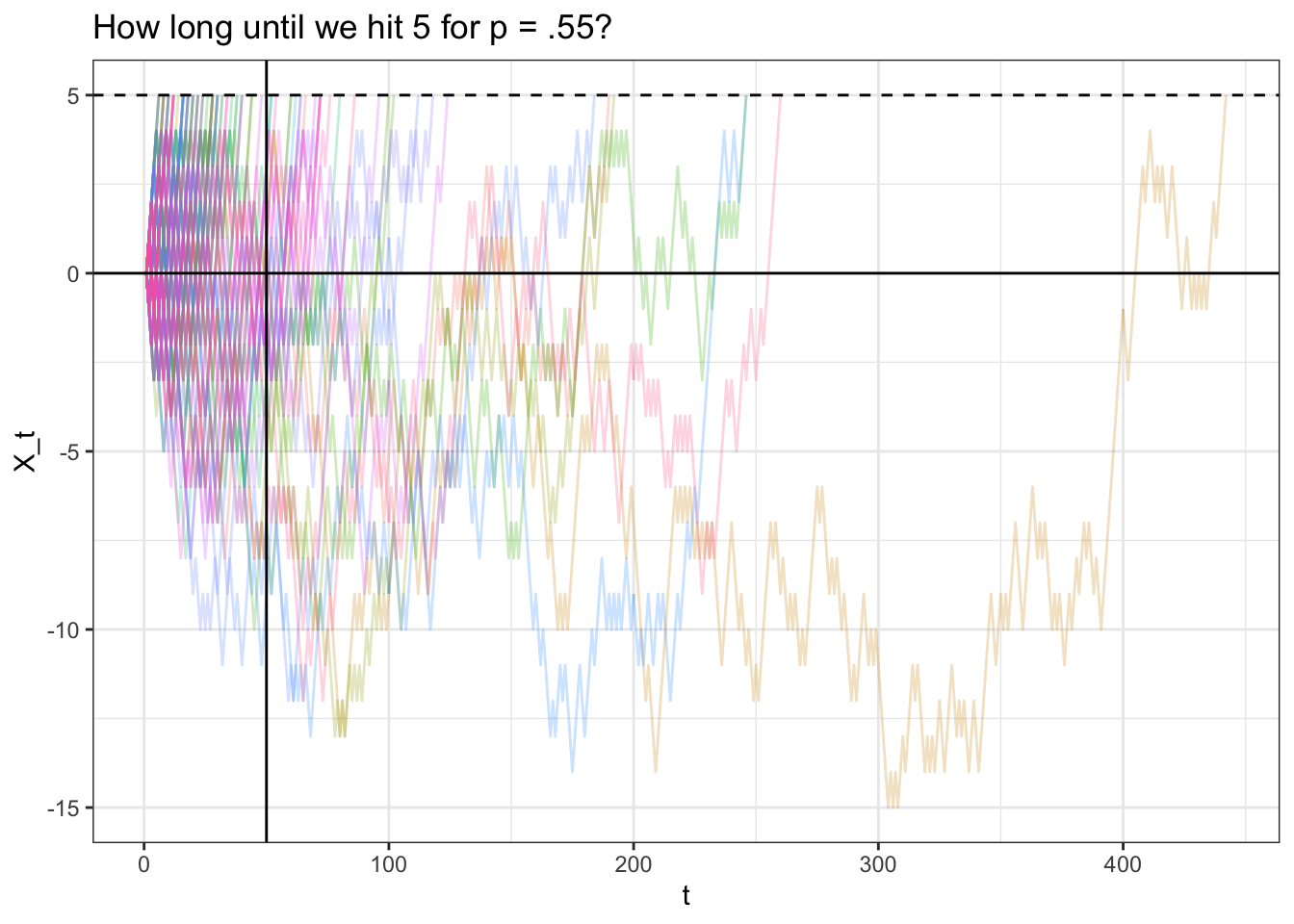
Note that our analytically result is very close to our empirical upshot of 49.48. The chart seems 'right-skewed'; many of the paths hit \(5\) long after \(t = fifty\), but nigh of the paths are clustered to the left of \(t = 50\) (they hit \(five\) well before \(t = 50\)); this balances out to a mean of \(50\).
Finally, here's a video walkthrough of this topic:
Click here to watch this video in your browser
Gambler's Ruin
Let'southward turn to a popular random walk, accurately titled 'the Gambler'south Ruin'; this problem will assist us to explore absorbing barriers and how they affect the behavior of random walks.
Nosotros take ii gamblers, named simply \(A\) and \(B\). There are \(N\) full dollars in the game; let \(A\) beginning with \(j\) dollars, which ways \(B\) starts with \(Due north - j\) dollars.
The Gamblers play repeated, ane round games. Each round, \(A\) wins with probability \(p\), and \(B\) wins with probability \(1 - p\), which we will characterization as \(q\) (the rounds are independent). If \(A\) wins, \(B\) gives one dollar to \(A\), and if \(B\) wins, \(A\) gives one dollar to \(B\). The game ends when one of the gamblers is ruined (they get to nothing dollars), which ways that the other gambler has all of the \(North\) dollars.
Let's play a simple game with 10 dollars (\(N = x\)) where \(A\) has the slight edge in each game \(p = .half dozen\) and both players kickoff with 5 dollars:
# replicate gear up.seed(0) FUN_ruin <- function(p, North, j) { # loop while (TRUE) { # interruption condition if (j[length(j)] == Due north || j[length(j)] == 0) { return(j) } # iterate const_play <- rbinom(1, 1, p) if (const_play == one) { j <- c(j, j[length(j)] + one) } if (const_play == 0) { j <- c(j, j[length(j)] - 1) } } } data <- data.table(A = FUN_ruin(p = .6, Due north = ten, j = five)) data$t <- 1 : nrow(information) ggplot(information, aes(ten = t, y = A)) + geom_line() + ggtitle("Gambler's Ruin") + theme_bw() + ylim(c(0, ten)) + geom_hline(yintercept = 0) + geom_hline(yintercept = 10) 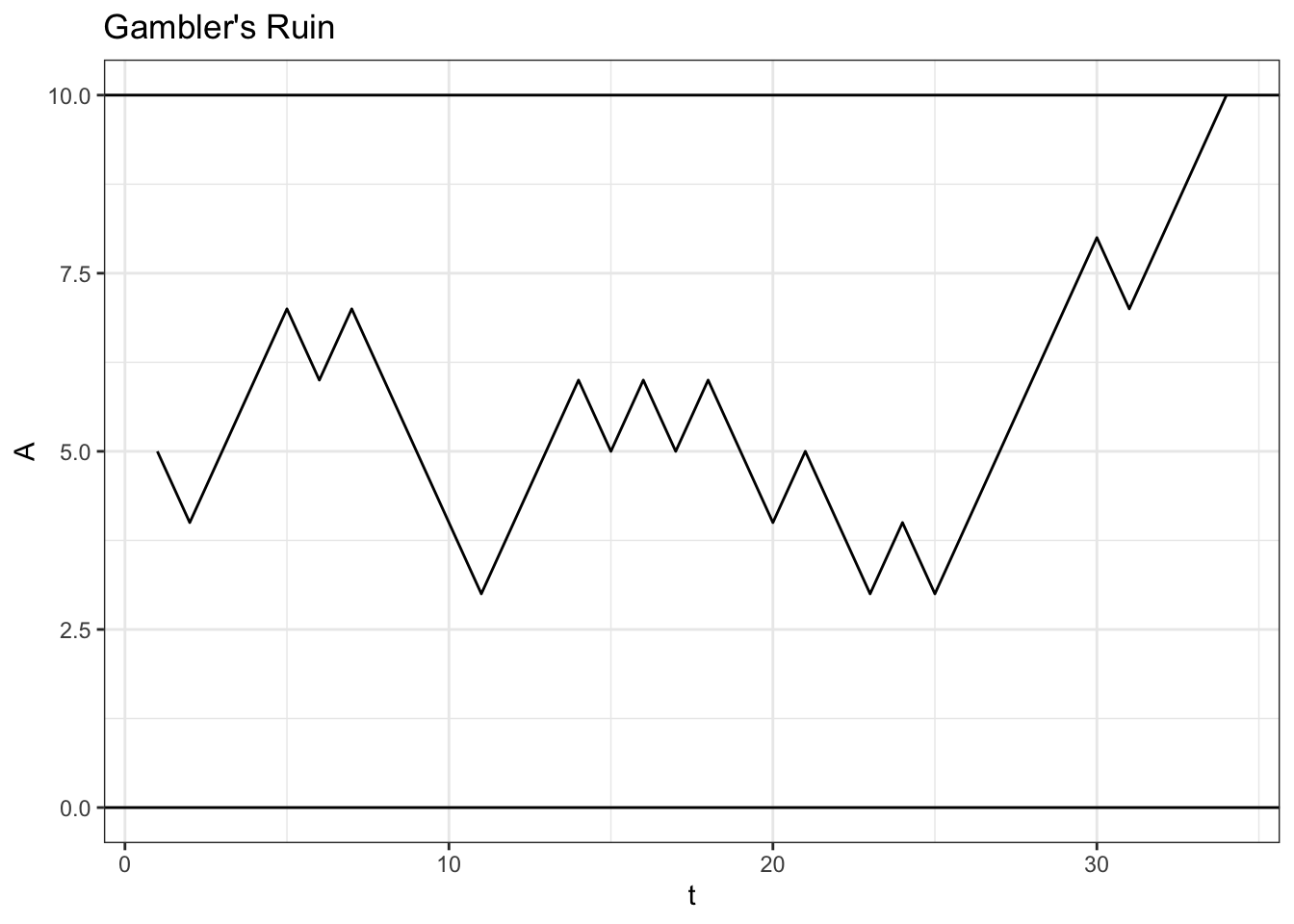
In this game, \(A\) won in the finish (fifty-fifty though it got a fiddling bit hairy in the middle for \(A\)!).
Win Probability
Naturally, some questions offset to arise. Of class \(A\) had the reward in the game above, since \(p = .6\). Does that mean \(A\) would win sixty% of games? What virtually if we started \(A\) with less money, say iv dollars (while \(B\) starts with 6)? Would \(A\) nonetheless exist favored?
All of these thoughts eddy down to a simple question: given \(p\) (the probability of \(A\) winning any one game) and \(N\) and \(j\) (the total number of dollars in the game and the total number of dollars that \(A\) starts out with) what is the probability that \(A\) wins the game and \(B\) is 'ruined?'
Allow's use some general note to solve this problem. We tin define, for a given game (where \(N\) and \(p\) are specified), \(w_j\) as the probability that \(A\) wins given that \(A\) has \(j\) dollars. Formally:
\[w_j = P(A \; wins | A \; starts \; at \; j \; dollars)\]
With the edge atmospheric condition:
\[w_0 = 0, \; \; w_N = 1\]
Because if \(A\) has \(0\) dollars so the game is over and he has lost, past definition, and if \(A\) has \(N\) dollars then the game is over and \(A\) has won, too by definition.
Since \(A\) has probability \(p\) of winning each game (independently) we tin write (again, using get-go pace analysis and thus workout on the outcome of the first game):
\[w_j = p \cdot w_{j + 1} + q \cdot w_{j - 1}\]
We're going to use a little trick here. Since \(p + q = i\), we tin plug \(p + q\) into the left hand side:
\[(p + q) \cdot w_j = p \cdot w_{j + 1} + q \cdot w_{j - ane}\]
And moving everything over:
\[0 = p \cdot w_{j + i} - (p + q) \cdot w_j + q \cdot w_{j - 1}\]
Let'southward suspension here. We are going to have to brand use of a '\(ii^{nd}\) guild homogeneous equation.' We're going to discuss the results of this tool, although we won't solve it here, since this blazon of mathematical tool is a bit outside of the telescopic of this volume.
For an equation of the form (with constants \(a\), \(b\) and \(c\)) we have:
\[aq_n + bq_{n - one} + cq_{due north - 2} = 0\]
If nosotros write a similar equation but with \(ten^n\) instead of \(q_n\):
\[ax ^ n + bx ^ {due north - 1} + cx ^ {n - 2} = 0\]
Dividing both sides by \(x^{n - two}\):
\[ax ^ two + bx+ c= 0\]
Nosotros can and then solve for \(x\) with the quadratic formula and we will get ii roots \(x_1\) and \(x_2\). Finally, this gives us:
\[q_n = c_1x_1^n + c_2x_2^n\]
Where \(c_1\) and \(c_2\) are constants. We can use the edge conditions of \(q_n\) to detect these constants.
This is a very nifty outcome, especially since we left off at:
\[p \cdot w_{j + 1} - (p + q) \cdot w_j + q \cdot w_{j - 1} = 0\]
Post-obit the steps laid out to a higher place, this becomes:
\[p \cdot ten^ii - (p + q) x + q = 0\]
We can use the quadratic formula here:
\[\frac{(p + q) \pm \sqrt{(p + q)^2 - 4pq}}{2p}\]
Nosotros know that \(p + q = 1\), merely allow's go out information technology as \(p + q\) for at present in the numerator and expand the \((p + q) ^ two\) term, since information technology may assist us factor this term down:
\[=\frac{(p + q) \pm \sqrt{p^two + q^two + 2pq - 4pq}}{2p}\]
\[=\frac{(p + q) \pm \sqrt{p^2 + q^two - 2pq}}{2p}\]
We accept that \((p^2 + q^2 - 2pq) = (p - q)^2 = (q - p)^ii\), and so nosotros can plug in:
\[=\frac{(p + q) \pm \sqrt{(p - q)^2}}{2p}\]
\[=\frac{(p + q) \pm (p - q)}{2p}\]
Remember that \(p - q = p - (1 - p) = 2p - 1\) (and \(q - p = 1 - 2p\), merely the flipping of signs doesn't matter much here because we have \(\pm\) anyways!), so we have:
\[=\frac{(p + q) \pm 2p - one}{2p}\]
Remembering that \((p + q) = 1\), nosotros have:
\[=\frac{i \pm 2p - 1}{2p}\]
Which gives us the two roots \(\frac{q}{p}\) and \(i\).
Now that nosotros have the two roots, we tin can movement to the side by side step in the process outlined above:
\[w_j = c_1 1^j + c_2(\frac{q}{p})^j\]
We can use the edge weather \(w_0 = 0\) and \(w_N = i\). First, we have:
\[w_0 = 0 = c_1 + c_2\]
Which tells us that \(c_1 = -c_2\). Adjacent, we have:
\[w_N = 1 = c_1 1^Northward + c_2(\frac{q}{p})^N\]
\[1 = c_1 + c_2 (\frac{q}{p})^N\]
Plugging in \(c_1 = -c_2\):
\[1 = -c_2 + c_2 (\frac{q}{p})^N\]
\[ane = c_2(-one + (\frac{q}{p})^Due north\] \[c_2 = \frac{1}{(\frac{q}{p})^N - ane}\]
And remembering \(c_1 = -c_2\):
\[c_1 = \frac{ane}{(ane - \frac{q}{p})^North}\]
Which ways we are left with:
\[w_j = \frac{1}{(1 - \frac{q}{p})^Due north} + \large(\frac{(\frac{q}{p})^j}{(\frac{q}{p})^N - 1}\big)\]
\[= \frac{1}{(1 - \frac{q}{p})^N} - \big(\frac{(\frac{q}{p})^j}{(one - \frac{q}{p})^North}\large)\] \[= \frac{i - (\frac{q}{p})^j}{1 - (\frac{q}{p})^N}\]
Voila! We now have a probability, for a given \(p\), \(j\) and \(N\), that \(A\) will win!
Sharp eyed readers may note that when \(q = p\), the higher up equation is undefined, since the denominator is \(1 - one = 0\). The above derivation, therefore, merely holds for \(q \neq p\).
If we accept \(p = q\), then our two roots higher up are yet \(1\) and \(\frac{q}{p} = 1\). That is, we have a double root at \(1\), which is non going to help us with our \(c_1\) and \(c_2\) equation. Hither, nosotros're going to exercise a bit of mathematical manus-waving that nosotros won't prove (since, again, differential equations is outside of the scope of this volume) and say that our equation for \(w_j\) in terms of \(c_1\) and \(c_2\) becomes:
\[w_j = c_1 \cdot j \cdot 1^j + c_21 ^j\]
\[= j c_1 + c_2\]
That is, since we have a double root at \(one\), we take that \(ane\) becomes the coefficient of both \(c_1\) and \(c_2\). Note that the hand-wavy part comes with the extra \(j\) term as a coefficient for \(c_1\); this is the part that we won't prove, since it requires an agreement of differential equations.
Anyways, carrying on as before, and using \(w_0 = 0\) and \(w_N = 1\), nosotros have…
\[0 = 0 \cdot c_1 + c_2\] \[c_2 = 0\]
…from the offset condition and…
\[one = North c_1 + c_2\] \[\frac{1}{N} = c_1\]
…for the second condition (since \(c_2 = 0\)). That means nosotros are just left with:
\[w_j = jc_1 = \frac{j}{N}\]
Voila! We now accept the probability of \(A\) winning for some \(j\) and \(Northward\), when \(p = one/2\). Note that this is intuitive; the larger that \(j\) is relative to \(Northward\) (i.e., the more than money that \(A\) starts out with relative to the total endowment), the college the probability that \(A\) wins (and, if \(j = N/ii\), we have that \(A\) has a \(1/2\) probability of winning, which makes sense because the game is perfectly symmetric!).
Anyways, let's investigate how this probability changes for unlike values of the input. Starting time, nosotros can fix the inputs \(Due north = 10\) and \(j = v\) and vary \(p\) to see how the win probability changes:
FUN_ruinprob <- function(N, p, j) { # edge cases if (p == 0) { return(0) } if (p == i) { return(1) } if (p == 1 / 2) { render(j / Due north) } q <- 1 - p return((1 - (q / p) ^ j) / (1 - (q / p) ^ N)) } # initiate parameters and generate probabilities N <- 10 j <- 5 p <- seq(from = 0, to = 1, by = .01) w <- sapply(p, office(x) FUN_ruinprob(N, x, j)) # visualize information <- data.tabular array(p = p, w = west) ggplot(information, aes(x = p, y = west)) + geom_point() + theme_bw() + ggtitle("Gambler's Ruin (N = 10, j = 5)") + xlab("p") + ylab("P(A Wins)") 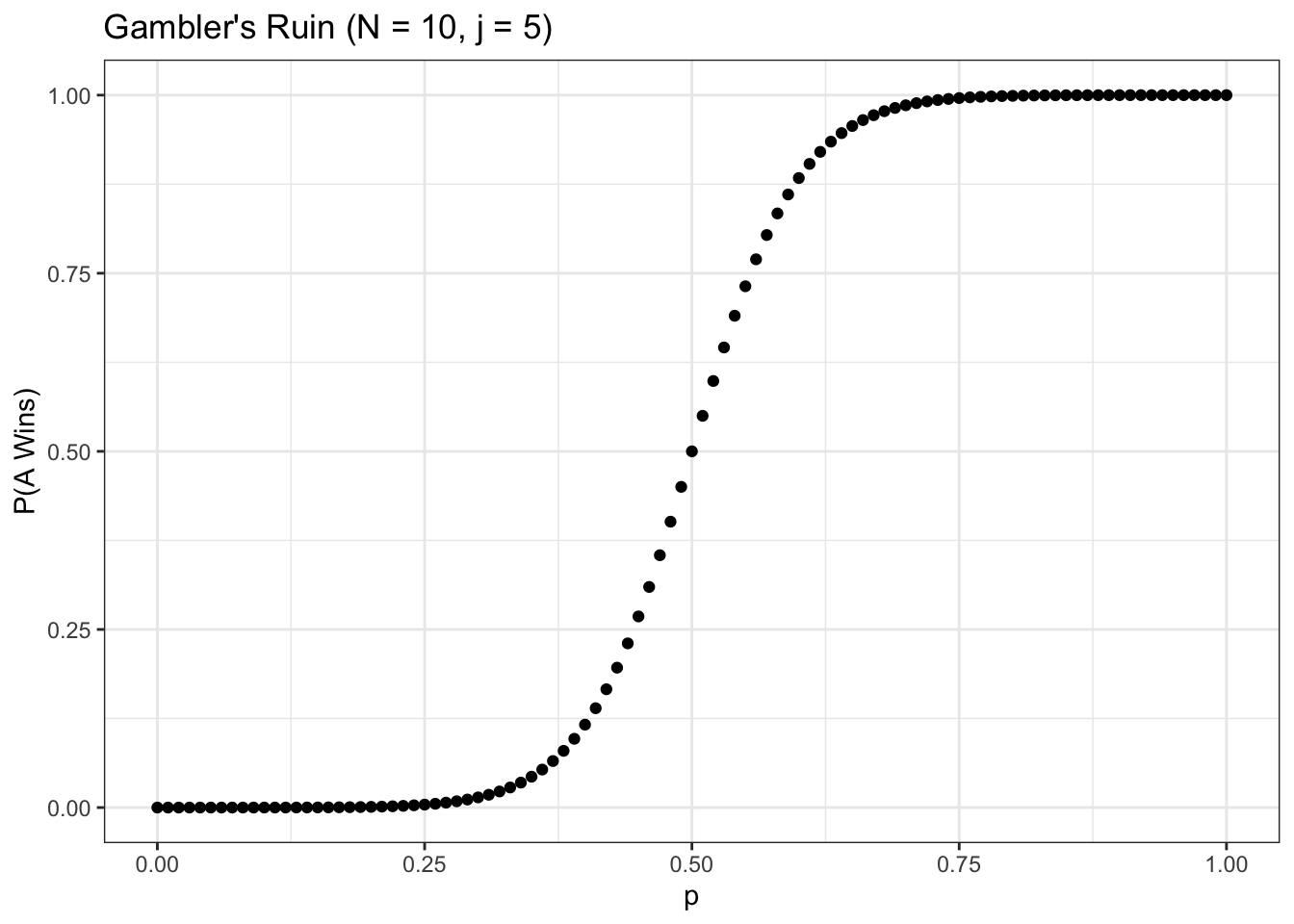
Unsurprisingly, as we increase \(p\), the probability that \(A\) wins rises rapidly (it gets very shut to \(i\) for \(p \geq .75\), and symmetrically very close to \(0\) for \(p \leq .25\)). As nosotros increment \(N\) (keeping \(j\) at \(N/two\)) the part gets even steeper:
# initiate parameters and generate probabilities North <- 50 j <- 25 p <- seq(from = 0, to = i, by = .01) w <- sapply(p, function(x) FUN_ruinprob(N, x, j)) # visualize information <- information.table(p = p, westward = westward) ggplot(data, aes(x = p, y = w)) + geom_point() + theme_bw() + ggtitle("Gambler'southward Ruin (North = 50, j = 25)") + xlab("p") + ylab("P(A Wins)") 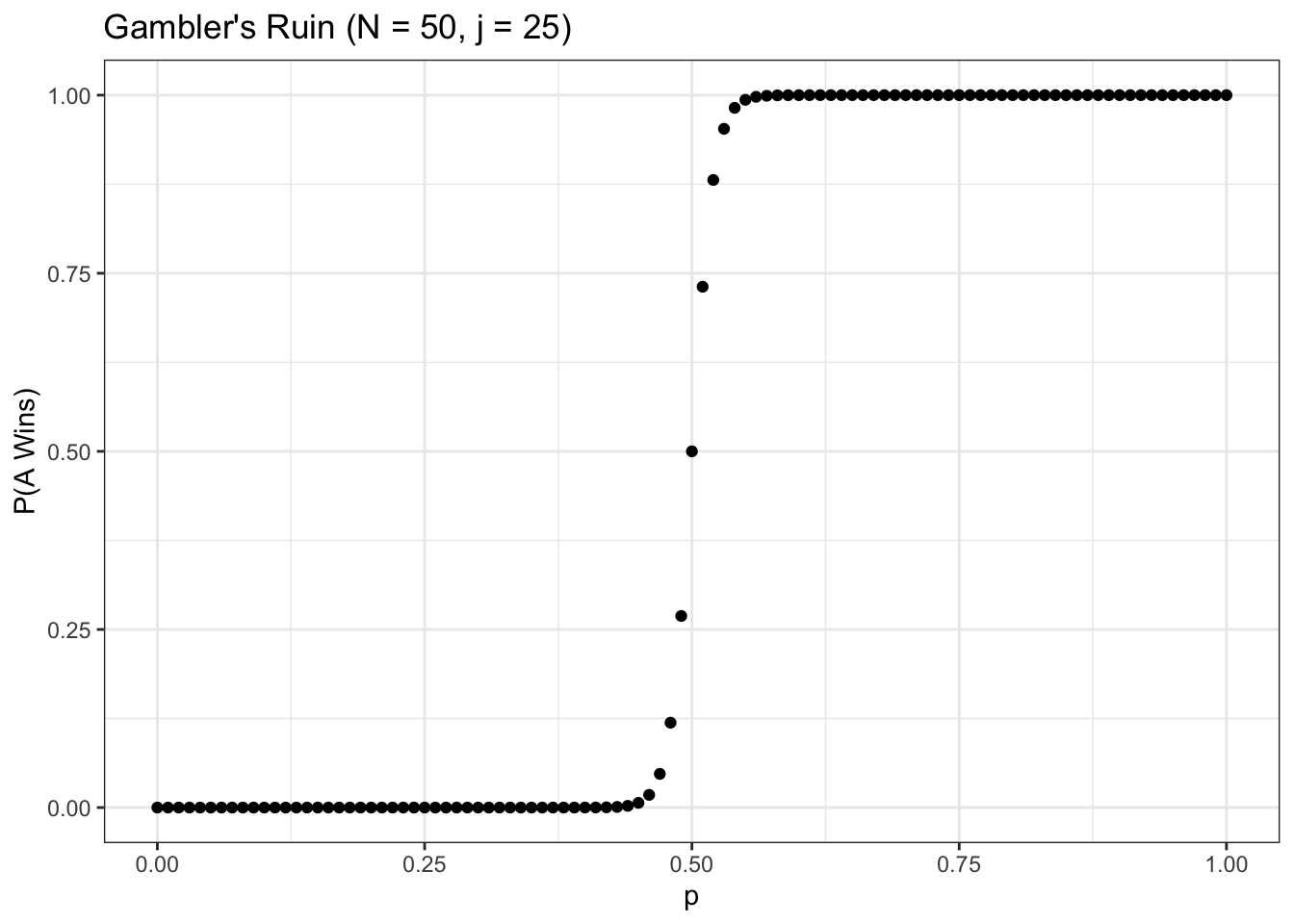
Note that, in this chart, the win probability for \(A\) goes to \(0\) or \(one\) much quicker. This is intuitive, since a larger \(N\) means that if \(A\) is the underdog (\(p < .5\)), and then \(A\) is less likely to 'pull off the upset' because the sample space is larger (\(A\) has to 'get lucky' for more rounds). A game with a lower \(N\) introduces a bit more randomness (i.due east., a chance for the underdog).
Let'due south endeavor fixing \(Due north\) at \(twenty\) and varying both \(j\) and \(p\) (nosotros tin use the aggrandize.grid role to get all of the values of \(j\) beyond all values of \(p\)).
# initiate parameters and generate probabilities Northward <- 10 j <- seq(from = 1, to = 9, past = 1) p <- seq(from = .1, to = .ix, by = .05) mat <- expand.filigree(j, p) w <- apply(mat, 1, role(x) FUN_ruinprob(N, x[two], x[i])) # visualize information <- information.tabular array(j = mat[ , i], p = mat[ , 2], westward = west) ggplot() + geom_point(data = data, aes(x = j, y = p, size = west)) + geom_text(information = data, aes(10 = j, y = p, label = round(west, ii), alpha = west), col = "ruddy") + theme_bw() + ggtitle("Gambler's Ruin (N = 10), P(A wins) = dot size") + xlab("j") + ylab("p") 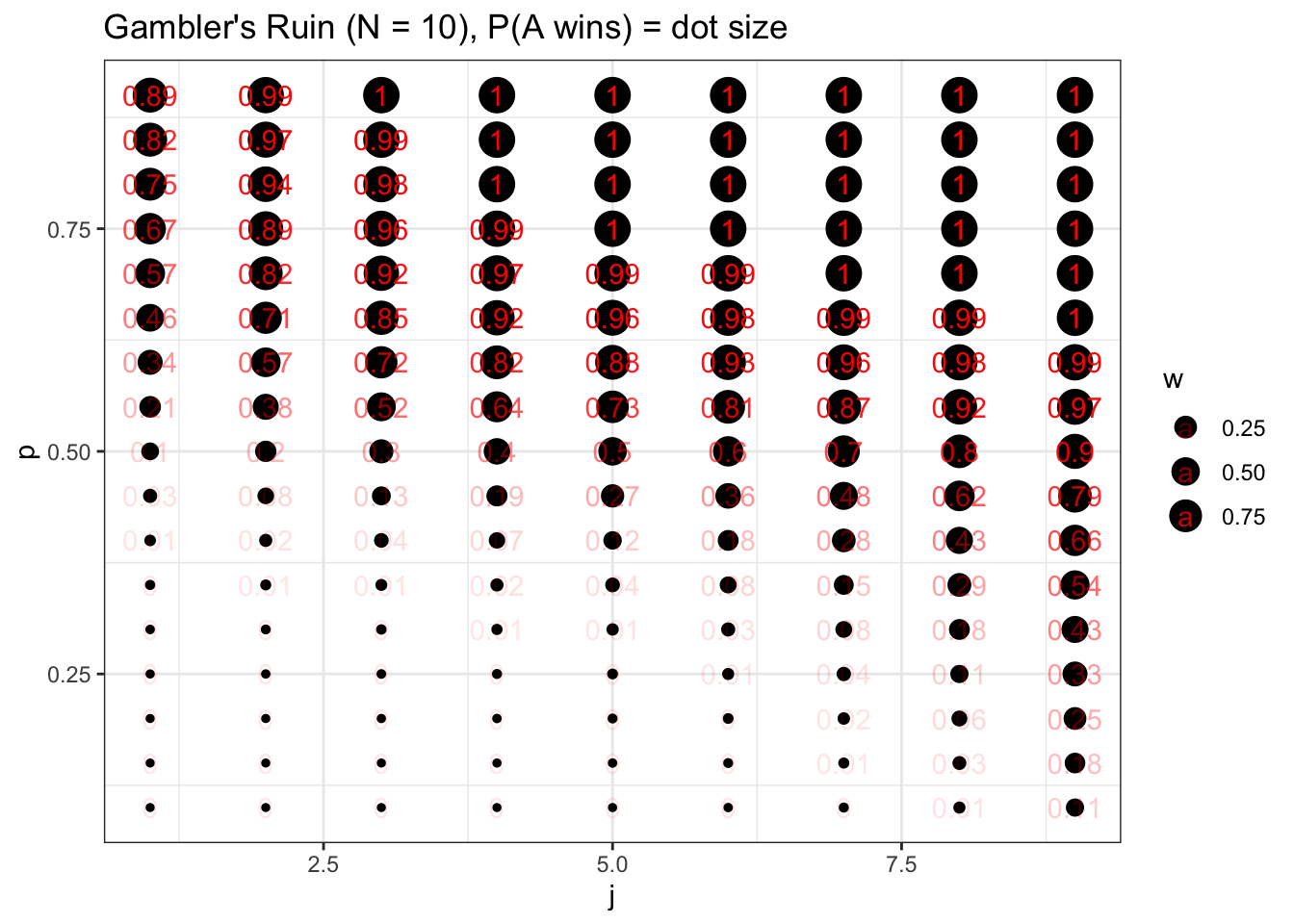
Here we vary \(j\) forth the x-axis and \(p\) along the y-axis, and study the win probability of \(A\) with the size of the bubble (we also overlay text that reports the win probability with geom_text). It's important to note here that \(p\) drives the win probability of \(A\) more than \(j\). We can run across this visually: the dots change more when nosotros move up and downwards than they do when we move left and right. Further, the edge cases are telling: when \(A\) simply starts with \(j = i\) dollars just has \(p = .9\) probability of winning each round, \(A\) has a \(.89\) probability of winning the unabridged game (the visual intuition hither is that \(A\) has a \(.9\) probability of winning the game and going to \(j = ii, \; p = .9\) on the graph, which has a \(.99\) win probability). That is, even though \(A\) is starting with 1 dollar and \(B\) is starting with the rest (ix dollars), \(A\) is still the overwhelming favorite. Symmetrically, of form, this means that if \(A\) starts with 9 dollars but has \(p = .1\), he only has a \(.11\) probability of winning the game.
Expected Game Length
Some other relevant question is a question of length: how long volition these games last? Let's consider a prepare-up every bit before: \(N\) dollars in the game, \(A\) starts with \(j\) dollars and has probability \(p\) of winning each circular. Ascertain \(M_j\) as the expected duration of the game if \(A\) starts with \(j\) dollars. Nosotros tin can write:
\[M_j = p(1 + M_{j + 1}) + q(1 + M_{j - ane})\]
Over again past beginning-step conditioning (we have probability \(p\) of moving to \(j + 1\) dollars for \(A\) - and thus having expectation \(M_{j + 1}\) - and probability \(q\) of moving to \(j - 1\) - and thus we move to expectation \(M_{j - i}\) - dollars for \(A\); we also add \(one\) because of that beginning pace that nosotros took).
Nosotros have uncomplicated edge cases: \(M_0 = M_N = 0\), since the game is over if \(A\) has \(0\) dollars or \(N\) dollars, by definition.
Anyways, let's expand this equation:
\[M_j = p(i + M_{j + one}) + q(i + M_{j - one})\]
\[M_j = p + pM_{j + 1} + q + q M_{j - one}\]
\[0 = pM_{j + one} - M_j + q M_{j - 1} + ane\]
This is a non-homogeneous 2d order difference equation; again, we're not going to delve deep into the proof backside the math here, so the approach may be a piffling hand-wavy.
We already saw that, for an equation of the course:
\[0 = pM_{j + ane} - M_j + q M_{j - i}\]
A solution is:
\[M_j = c_1 + (\frac{q}{p})^jc_2\]
For a not-homogeneous difference equation, we accept this result and add together it to a detail solution of:
\[0 = pM_{j + 1} - M_j + q M_{j - ane} + 1\]
I solution that works is \(M_j = \frac{j}{q - p}\). We can plug this in:
\[0 = \frac{p(j + one)}{q - p} - \frac{j}{q - p} + \frac{q(j - 1)}{q - p} + one\]
Multiplying both sides by \((q - p)\), we get:
\[0 = pj + p - j + qj - q + q - p\]
\[= pj - j + qj\]
\[= j - j\] \[= 0\]
Excellent! So, \(\frac{j}{q - p}\) is a item solution here. Adding to this to our full general solution from earlier, nosotros go:
\[M_j = c_1 + (\frac{q}{p})^jc_2 + \frac{j}{q - p}\]
Using the boundary condition \(M_0 = 0\), nosotros get:
\[0 = c_1 + c_2\]
\[c_1 = -c_2\]
And the 2d purlieus condition \(M_N = 0\), we get:
\[0 = c_1 + c_2(\frac{q}{p})^Northward + \frac{N}{q - p}\]
Plugging in \(c_2 = -c_1\):
\[0 = c_1 - c_1(\frac{q}{p})^Northward + \frac{N}{q - p}\]
\[-\frac{Due north}{q - p} = c_1(1 - (\frac{q}{p})^N)\]
\[c_1 = \frac{-\frac{Due north}{q - p}}{1 - (\frac{q}{p})^N}\]
And therefore:
\[c_2 = \frac{\frac{N}{q - p}}{one - (\frac{q}{p})^N}\]
Plugging in for:
\[M_j = c_1 + (\frac{q}{p})^jc_2 + \frac{j}{q - p}\]
\[M_j = \frac{-\frac{N}{q - p}}{1 - (\frac{q}{p})^N} + (\frac{q}{p})^j \big(\frac{\frac{Northward}{q - p}}{one - (\frac{q}{p})^N}\big) + \frac{j}{q - p}\]
First-class! Unfortunately, there's not a lot of algebra we can exercise to reduce this. We can write it in a more elegant way by splitting out the constants:
\[c_2 = \frac{N}{(q - p)\big(1 - (\frac{q}{p})^N)}\] \[c_1 = -c_2\]
\[M_j = c_1 + c_2 (\frac{q}{p})^2 + \frac{j}{q - p}\]
Where, remember, \(M_j\) is the expected length of a Gambler'southward Ruin game with \(North\) total dollars where \(A\) starts with \(j\) dollars and has probability \(p\) of winning each circular.
Note that, again, this is undefined for \(p = q\) (each of the terms would be dividing by \(0\)). We tin can go back to our original relation:
\[0 = pM_{j + one} - M_j + q M_{j - 1} + 1\]
And retrieve from our solution of the win probability that a solution for an equation of the class \(0 = pM_{j + 1} - M_j + q M_{j - 1}\) where \(p = q\) is:
\[M_j = c_1 + c_2 j\]
Nosotros now demand a particular solution to \(0 = pM_{j + one} - M_j + q M_{j - 1} + 1\). Nosotros can try \(-j^ii = M_j\):
\[0 = -p(j + 1)^2 + j^2 + -q(j - 1)^2 + i\] \[0 = -pj^2 - 2pj - p + j^2 - qj^ii + 2qj - q + 1\] \[0 = -j^2- p + j^two - q + 1\] \[0 = -j^2 + j^2 - 1 + 1\] \[0 = 0\]
Excellent! Information technology looks like \(-j^2\) is a particular solution, which means, continuing as we did in the \(p \neq q\) case, we accept:
\[M_j = c_1 + c_2 j - j^2\]
Let's now use our purlieus conditions \(M_0 = 0\) and \(M_N = 0\). Showtime, we have:
\[M_0 = 0 = c_1\]
And second, we have:
\[M_N = 0 = c_1 + Nc_2 - N^two\]
Plugging in \(c_1 = 0\) and rearranging, we have:
\[c_2 = N\]
Plugging in \(c_1\) and \(c_2\) in our equation for \(M_j\), nosotros have:
\[M_j = Nj - j^two = j(N - j)\]
This is the expected length of a game when \(p = q = 1/2\). We can apace see for what value of \(j\) this is maximized by deriving w.r.t. \(j\), setting equal to nix and solving for \(j\):
\[M_j^{\prime} = N - 2j = 0\] \[j = \frac{N}{2}\]
This is intuitive; if the game is equally counterbalanced, then the game volition be longest if \(j\) is half of \(N\) (if both players have an equal chance of winning each round, then nosotros expect the game to be longest if both players have an equal corporeality of money!).
We tin code upwardly this expectation and see how it changes every bit we vary the parameters:
FUN_ruinlength <- function(N, j, p) { # p = 1 / 2 case if (p == 1 / two) { render(j * (Northward - j)) } # other instance q <- 1 - p c_2 <- Northward / ((q - p) * (ane - (q / p) ^ N)) c_1 <- -c_2 return(c_1 + c_2 * (q / p) ^ j + j / (q - p)) } # initiate parameters and generate probabilities N <- ten j <- seq(from = one, to = ix, by = 1) p <- seq(from = .one, to = .9, by = .05) mat <- aggrandize.grid(j, p) w <- apply(mat, one, part(ten) FUN_ruinlength(N, x[1], 10[2])) # visualize data <- information.table(j = mat[ , 1], p = mat[ , 2], w = due west) ggplot() + geom_point(data = information, aes(x = j, y = p, size = w)) + theme_bw() + ggtitle("Gambler's Ruin (N = x), Due east(Game Length) = dot size") + xlab("j") + ylab("p") 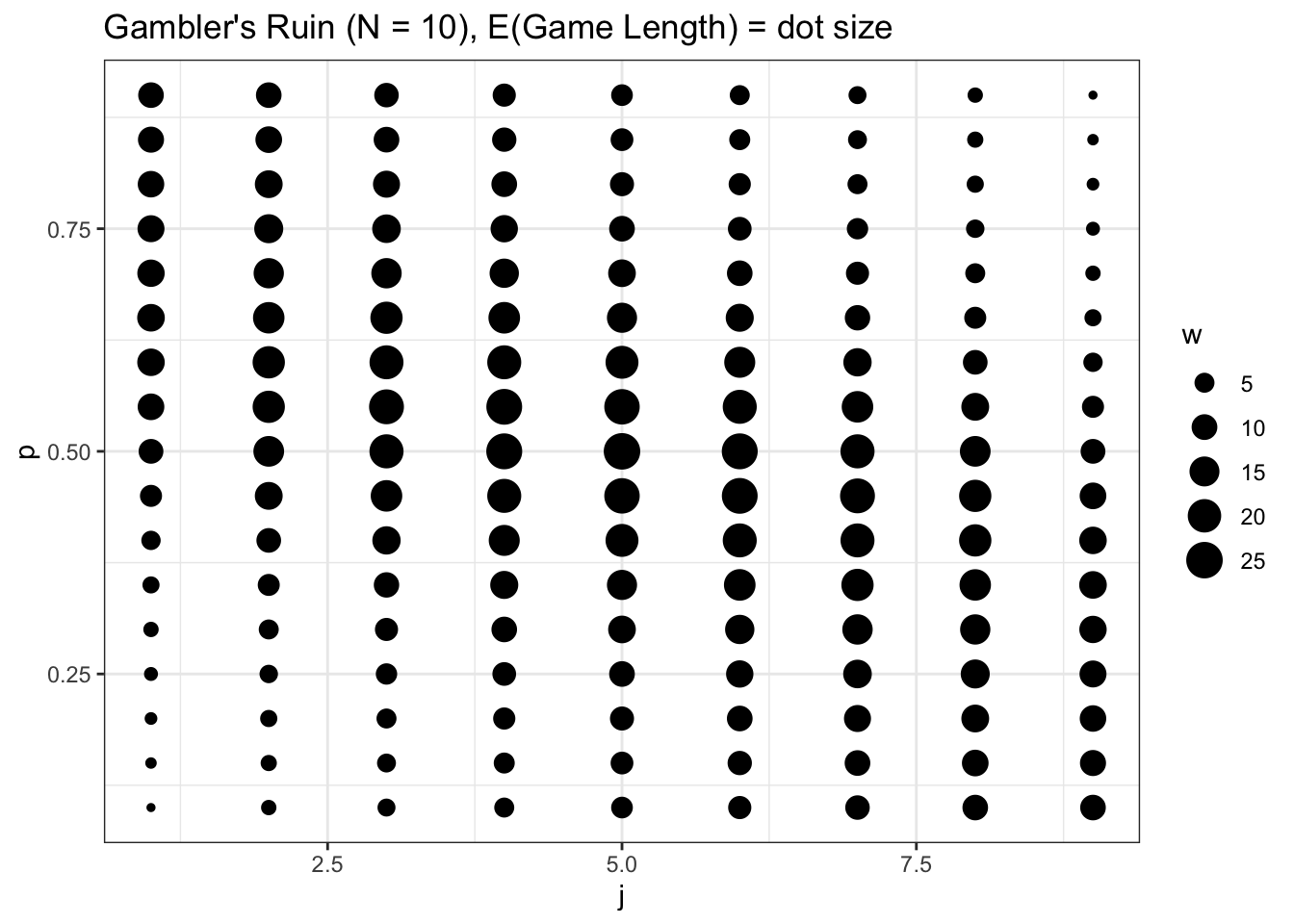
Intuitively, the closer that we become to a 'off-white game' (\(j = 5\), which means that the players carve up the total amount of coin \(N = 10\), and \(p = one/ii\), which means that each thespian has an equal probability of winning each round), the longer the games are expected to final. This time, interestingly, it seems that \(p\) and \(j\) both touch on the expected game length a similar amount; unlike the previous win probability chart, the size of the dots don't modify more drastically when we look up and downward vs. when we expect left and correct.
Finally, we tin examination that our solution actually makes sense by playing many Gambler'southward Ruin games with some initial parameters and checking that the average game length is close to our analytically result. We can simulate this easily with the FUN_ruin role defined earlier in this chapter:
# replicate set.seed(0) # initialize parameters and generate results p <- 1 / 3 j <- five N <- ten results <- replicate(FUN_ruin(Due north = N, p = p, j = j), northward = 1000) results <- unlist(lapply(results, function(10) length(x) - 1)) # should match mean(results); FUN_ruinlength(Northward, j, p) ## [1] thirteen.818 ## [1] xiv.09091 bledsoewasing1988.blogspot.com
Source: https://bookdown.org/probability/bookdown-demo/random-walks.html
0 Response to "Suppose a Random Walk Start at the Origin Probability That It Will Ever Touch the Xaxis Again"
Post a Comment